문제정의
- 손글씨 숫자(0~9)를 분류하는 모델을 만들어보자
- 이미지 데이터의 형태를 이해해보자
데이터 수집
In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
In [2]:
# 데이터 가져오기
data = pd.read_csv('./data/digit_train.csv')
In [3]:
# 데이터 크기 확인
data.shape
Out[3]:
(42000, 785)In [4]:
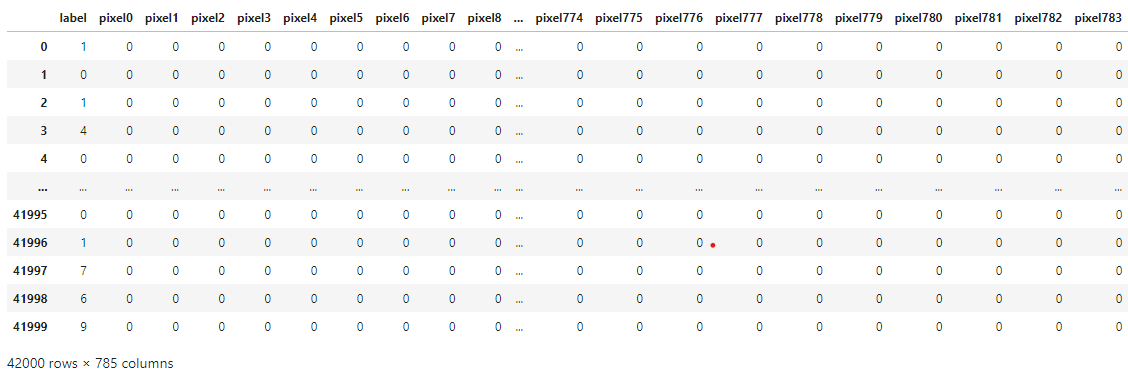
data.head()
# label : 정답
# pixel0 ~ pixel783 : 문제 (28*28 이미지 데이터)
Out[4]:

In [5]:
# 데이터 시각화 --> 이미지 데이터로 첫번째 행의 label을 제외한 모든 컬럼 가져오기
img0 = data.iloc[0, 1:]
img0.shape
Out[5]:
(784,)In [6]:
img0.values # rgb(0 ~ 255)
Out[6]:

In [7]:
# 리스트 자료형을 28*28의 2차원으로 변환
img0_reshape = img0.values.reshape(28,28)
In [8]:
# img0 이미지 하나를 그려보기
plt.imshow(img0_reshape, cmap='gray')
Out[8]:
<matplotlib.image.AxesImage at 0x1c408394970>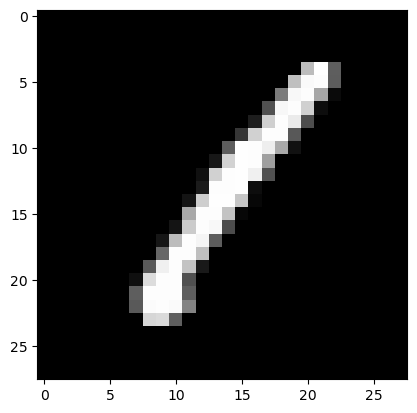
In [9]:
# 7777행의 데이터 꺼내와서 - 값 확인 - 2차원 변환 - 이미지 그려보기 - 어떤 숫자인지 확인
img7777 = data.iloc[7777, 1:]
img7777_reshape = img7777.values.reshape(28,28)
plt.imshow(img7777_reshape, cmap='gray')
# plt.show() # 불필요한 text 정보를 출력하지 않는 코드
Out[9]:
<matplotlib.image.AxesImage at 0x1c4084652d0>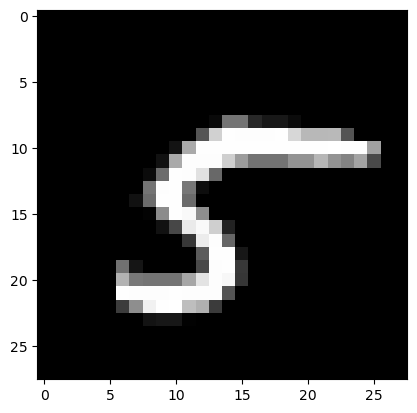
학습을 위한 데이터 분리
- 학습 7 : 테스트 3
- random_state : 7
In [10]:
data
Out[10]:
In [11]:
X = data.iloc[:, 1 : ] # 문제 - 2차원 데이터프레임 형태 [[ ]]
y = data.iloc[:, 0] # 정답 - 1차원 시리즈 형태
In [12]:
# 크기 확인
X.shape, y.shape
Out[12]:
((42000, 784), (42000,))In [13]:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=7)
In [14]:
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
(29400, 784)
(12600, 784)
(29400,)
(12600,)
모델 선택
- KNN
- Logistic Regression
- SVM
In [15]:
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
# 모델 생성
knn_model = KNeighborsClassifier()
logi_model = LogisticRegression()
svm_model = LinearSVC()
학습 및 평가
In [16]:
# 학습
knn_model.fit(X_train, y_train)
logi_model.fit(X_train, y_train)
svm_model.fit(X_train, y_train)
# 평가
print('KNN : ', knn_model.score(X_test, y_test))
print('Logistic : ', logi_model.score(X_test, y_test))
print('SVM : ', svm_model.score(X_test, y_test))
KNN : 0.9645238095238096
Logistic : 0.9138095238095238
SVM : 0.8468253968253968
데이터 스케일링 적용
- 이미지 픽셀정보 : 0 ~ 255로 최소/최대가 고정되어 있는 데이터
- MinMaxScaler를 사용하여 0 ~ 1 사이의 값으로 모든 픽셀을 조정
- 스케일링의 효과 확인하기
- 학습(연산) 속도 개선
- 거리기반으로 예측하는 KNN 모델 --> 거의 변화가 없었음.
- KNN 모델 : 모든 데이터의 대한 거리를 계산, 데이터가 많을수록 속도가 느려짐
In [17]:
from sklearn.preprocessing import MinMaxScaler
In [18]:
scaler = MinMaxScaler() # 0 ~ 1 사이로 변환
In [19]:
scaler.fit(X_train) # 현재 데이터 분포의 최소/최대 값 확인
# 변환하는 기준 값을 X_train으로 추출
Out[19]:
MinMaxScaler
MinMaxScaler()In [20]:
X_train
Out[20]:

In [21]:
# 문제데이터에 스케일링 적용
X_train_scale = scaler.transform(X_train)
X_test_scale = scaler.transform(X_test)
In [22]:
# 스케일링이 적용된 데이터로 다시 학습
knn_model.fit(X_train_scale, y_train)
logi_model.fit(X_train_scale, y_train)
svm_model.fit(X_train_scale, y_train)
# 스케일링이 적용된 데이터로 변화값 확인
print('KNN : ', knn_model.score(X_test_scale, y_test))
print('Logistic : ', logi_model.score(X_test_scale, y_test))
print('SVM : ', svm_model.score(X_test_scale, y_test))
KNN : 0.9644444444444444
Logistic : 0.9169047619047619
SVM : 0.9093650793650794
In [23]:
# 데이터 스케일링전 수치
# KNN : 0.9645238095238096
# Logistic : 0.9138095238095238
# SVM : 0.8741269841269841
평가지표
- 회귀 : 오차를 기반으로 하는 평가지표 사용(MSE, R2score)
- 분류 : 맞춘 개수를 기반으로 평가지표를 사용
- 정확도(Accuracy) : 전체 데이터중에 정확히 맞춘 비율
- 재현율(Recall) : 실제 양성중에서 정확히 맞춘 비율
- 정밀도(Precision) : 예측 양성중에서 정확히 맞춘 비율
- F1-score : 정밀도와 재현율의 조화평균
- SVM : 초평면(결정경계)을 기준으로 소프트벡터의 마진(거리)이 클수록 좋은 결정경계
In [24]:
# 평가지표 라이브러리 불러오기
from sklearn.metrics import confusion_matrix
In [25]:
# 스케일링이 적용된 테스트데이터로 예측값 만들기
# 로지스틱분류 사용
pre = logi_model.predict(X_test_scale)
In [26]:
# confusion_matrix(실제값, 예측값)
test_conf = confusion_matrix(y_test, pre)
test_conf
Out[26]:
array([[1207, 0, 4, 4, 3, 13, 6, 3, 7, 2],
[ 0, 1406, 7, 7, 1, 4, 1, 2, 8, 4],
[ 7, 11, 1112, 23, 15, 3, 11, 19, 22, 8],
[ 7, 2, 39, 1152, 1, 46, 1, 11, 28, 12],
[ 3, 18, 10, 2, 1140, 1, 13, 10, 9, 44],
[ 11, 7, 16, 41, 15, 936, 17, 7, 29, 9],
[ 13, 4, 8, 1, 16, 16, 1157, 1, 7, 2],
[ 1, 11, 13, 4, 7, 1, 2, 1216, 3, 48],
[ 9, 38, 8, 36, 9, 27, 6, 1, 1089, 24],
[ 8, 8, 2, 10, 36, 8, 0, 44, 11, 1138]],
dtype=int64)In [27]:
from sklearn.metrics import classification_report
# classification_report - 분류평가지표
In [28]:
# classification_report(실제값, 예측값)
print(classification_report(y_test, pre))
precision recall f1-score support
0 0.95 0.97 0.96 1249
1 0.93 0.98 0.95 1440
2 0.91 0.90 0.91 1231
3 0.90 0.89 0.89 1299
4 0.92 0.91 0.91 1250
5 0.89 0.86 0.87 1088
6 0.95 0.94 0.95 1225
7 0.93 0.93 0.93 1306
8 0.90 0.87 0.89 1247
9 0.88 0.90 0.89 1265
accuracy 0.92 12600
macro avg 0.92 0.92 0.92 12600
weighted avg 0.92 0.92 0.92 12600
- support : 데이서의 갯수
- accuracy : 로직스틱회귀의 예측성능 92%이지만, 각 숫자(클래스)가 나온 확률의 수치값은 다름
- f1-score : 정밀도와 재현율의 조화평균 --> 정밀도와 재현율을 고려한 수치값 --> 수치가 높은게 두 분류지표(정밀도, 재현율)도 높음을 알 수 있음
- macro avg : 정밀도, 재현율, f1-score를 구해서 각각 평균을 낸 것 --> 분류모델이 각 클래스에 대해 얼마나 평균적으로 잘 동작하는지 알고싶을 때 사용
- weighted avg(가중평균) : 각 클래스의 중요도, 영향도(빈도) 등에 따라서 가중치를 곱해서 구해지는 평균
예측
In [29]:
# index 7번째 데이터 가져오기
img7 = X_test_scale[7]
In [30]:
logi_model.predict([img7])
Out[30]:
array([1], dtype=int64)In [31]:
# 실제 정답 확인
y_test.iloc[7]
Out[31]:
1In [32]:
svm_model.predict([img7])
Out[32]:
array([1], dtype=int64)In [33]:
logi_model.predict_proba(X_test_scale[7:8]) # 7번째 값(0 ~ 9) 숫자가 1일 확률
# svm은 predict_proba 없음
Out[33]:
array([[3.73323833e-10, 9.88049149e-01, 2.75926406e-04, 3.35151433e-03,
2.15892443e-06, 7.28083512e-05, 1.06545842e-05, 6.20899060e-03,
1.35662821e-04, 1.89313425e-03]])In [34]:
img7 = X_test.iloc[7]
plt.imshow(img7.values.reshape(28,28), cmap='gray')
Out[34]:
<matplotlib.image.AxesImage at 0x1c40a7ed000>
- 낮은 재현율 높은 정밀도 : 모델이 한 번 예측할 때마다 비용이 많이 들 경우 적합 ==> 의약실험, 모델이 예측의 리스크/비용이 큰 경우, 아이에게 유익한 영상만 보여주고 싶을 때
- 높은 재현율 낮은 정밀도 : 실제 사건(상황)에 대한 리스크가 큰 경우 적합 ==> 감시카메라를 이용해 좀도둑을 걸러내는 상황, 암환자 판정, 스팸문자
- 같은 정확도일 때 애매한 것들을 사용하지 않겠다 ==> 높은 정밀도
- 같은 정확도일 때 애매한 것들을 사용하겠다 ==> 높은 재현율
- 상황에 맞게 평가지표를 적용
- best : 높은 재현율, 높은 정밀도
- ROC 곡선
- 임계값을 0 ~ 1 까지 변화시켜가면서
- x축 : 가짜 양성 비율(FPR), y축 : 진짜 양성 비율(TPR)을 표시한 곡선
- 임계값 변화에 따라 양성/음성 분류가 달라짐, ROC 곡선도 달라짐
- ROC 곡선 아래 면적 - AUC(Area Under Curve)
- AUC의 값이 1에 가까울수록 분류모델의 성능이 좋다고 평가
- 0.5를 기준으로 위쪽으로 갈수록 좋음.